Estadistica
viernes, 26 de junio de 2015
1.1 Manejo de la Información
Manejo de la Información Estadística”
La investigación cuya finalidad es: el análisis o experimentación de situaciones para el descubrimiento de nuevos hechos, la revisión o establecimiento deteorías y las aplicaciones prácticas de las mismas, se basa en los principios de Observación y Razonamiento y necesita en su carácter científico el análisis técnico de Datos para obtener de ellosinformación confiable y oportuna. Este análisis de Datos requiere de la Estadística como una de sus principales herramientas, por lo que los investigadores de profesión y las personas que de una y otraforma la realizan requieren además de los conocimientos especializados en su campo de actividades, del manejo eficiente de los conceptos, técnicas y procedimientos estadísticos
El manejo de información es un proceso que exige informarse e informar. Es decir, exige construir, primero, una representación de una determinada realidad con los datos que adquirimos de ella para poder darla a conocer, disponiendo esa representación al alcance de los demás o comunicarla."
CUANDO HABLAMOS DE EL MANEJO DE LA INFORMACION, PODEMOS AGRAGAR LAS CARACTERISTICAS DE LAS MISMAS. Es un proceso dinámico: porque está en continuo movimiento, inevitable: porque se requiere para la transmisión de significados, irreversible: porque una vez realizada, no puede regresar, borrarse o ignorarse. Bidireccional: porque existe una respuesta en ambas direcciones. Verbal y no verbal: porque implica la utilización de ambos lenguajes.Con esta información podemos entender como es que hoy en día internet se volvió en un medio de comunicación tan importante ya que permite comunicarnos permanentemente y en forma instantánea.
El manejo de la información, es sin duda un factor letal que debe considerar el usuario a la hora de navegar en la red. El mayor temor suele ser la privacidad, y por más que se intente siguen habiendo problemas e inseguridad. Es una ironía, sin embargo si se considera que los consumidores dicen que quieren privacidad online, aunque a menudo se comportan de un modo contradictorio, enviando por ejemplo información personal y fotos a páginas web públicas. Las empresas insisten en que protegerán la privacidad, pero a veces no lo consiguen. Y a todo el mundo le preocupa una mayor regulación por parte del Gobierno; de hecho, a alguna gente le preocupa más el abuso potencial del Gobierno que el abuso potencial de las corporaciones.
“Nuestro concepto de privacidad se basa en la idea de quién es usted. Pero tenemos que pensar ahora también en lo que usted hace. El debate en torno a la privacidad y la estructura básica de la cuestión cambiaron para siempre”.Claramente, hoy en día nuestra información no solo se refiere a nuestros datos personales, nuestro nombre, dirección, mail, teléfono, datos bancarios, sino que también nuestra información esta compuesta por nuestros gustos, por nuestros modos de actuar, por nuestros vinculos y por absolutamente todo lo que nos rodea. Hoy en día las empresas y páginas web no solo saben quienes somos sino que también estan al tanto de lo que hacemos, lo que nos gusta, y peor aún, hasta pueden planear y deducir lo que haremos y lo que nos gustará en un futuro.
3.5 varianza
varianza
En teoría de probabilidad, la varianza (que suele representarse como ) de una variable aleatoria es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media.
) de una variable aleatoria es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media.
Está medida en unidades distintas de las de la variable. Por ejemplo, si la variable mide una distancia en metros, la varianza se expresa en metros al cuadrado. La desviación estándar es la raíz cuadrada de la varianza, es una medida de dispersión alternativa expresada en las mismas unidades de los datos de la variable objeto de estudio. La varianza tiene como valor mínimo 0.
Hay que tener en cuenta que la varianza puede verse muy influida por los valores atípicos y no se aconseja su uso cuando las distribuciones de las variables aleatorias tienen colas pesadas. En tales casos se recomienda el uso de otras medidas de dispersión más robustas.
 o, simplemente σ2), como
o, simplemente σ2), como
 de n valores de ella, de entre todos los estimadores posibles de la varianza de la población de partida, existen dos de uso corriente:
de n valores de ella, de entre todos los estimadores posibles de la varianza de la población de partida, existen dos de uso corriente:
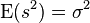 , s2 es un estadístico insesgado de
, s2 es un estadístico insesgado de  . Además, si se cumplen las condiciones necesarias para la ley de los grandes números, s2 es un estimador consistente de
. Además, si se cumplen las condiciones necesarias para la ley de los grandes números, s2 es un estimador consistente de  .
.
Más aún, cuando las muestras siguen una distribución normal, por el teorema de Cochran,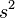 tiene la distribución chi-cuadrado:
tiene la distribución chi-cuadrado:

 .
.


En teoría de probabilidad, la varianza (que suele representarse como
 ) de una variable aleatoria es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media.
) de una variable aleatoria es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media.Está medida en unidades distintas de las de la variable. Por ejemplo, si la variable mide una distancia en metros, la varianza se expresa en metros al cuadrado. La desviación estándar es la raíz cuadrada de la varianza, es una medida de dispersión alternativa expresada en las mismas unidades de los datos de la variable objeto de estudio. La varianza tiene como valor mínimo 0.
Hay que tener en cuenta que la varianza puede verse muy influida por los valores atípicos y no se aconseja su uso cuando las distribuciones de las variables aleatorias tienen colas pesadas. En tales casos se recomienda el uso de otras medidas de dispersión más robustas.
Definición
Si tenemos un conjunto de datos de una misma variable, la varianza se calcula de la siguiente forma: : cada dato
: cada dato : El número de datos
: El número de datos : la media aritmética de los datos
: la media aritmética de los datos
Variable aleatoria
Aplicando este concepto a una variable aleatoria con media μ = E[X], se define su varianza, Var(X) (también representada como o, simplemente σ2), como
o, simplemente σ2), comoCaso continuo
Si la variable aleatoria X es continua con función de densidad f(x), entoncesCaso discreto
Si la variable aleatoria X es discreta con pesos x1 ↦ p1, ..., xn ↦ pn y n es la cantidad total de datos, entonces tenemos: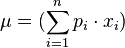 .
.
Ejemplos
Distribución exponencial
La distribución exponencial de parámetro λ es una distribución continua con soporte en el intervalo [0,∞) y función de densidadDado perfecto
Un dado de seis caras puede representarse como una variable aleatoria discreta que toma, valores del 1 al 6 con probabilidad igual a 1/6. El valor esperado es (1+2+3+4+5+6)/6 = 3,5. Por lo tanto, su varianza es:Propiedades de la varianza
Algunas propiedades de la varianza son: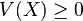
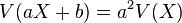 siendo a y b números reales cualesquiera. De esta propiedad se deduce que la varianza de una constante es cero, es decir,
siendo a y b números reales cualesquiera. De esta propiedad se deduce que la varianza de una constante es cero, es decir, 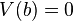
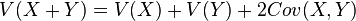 , donde Cov(X,Y) es la covarianza de X e Y.
, donde Cov(X,Y) es la covarianza de X e Y.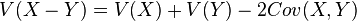 , donde Cov(X,Y) es la covarianza de X e Y.
, donde Cov(X,Y) es la covarianza de X e Y.
Varianza muestral
En muchas situaciones es preciso estimar la varianza de una población a partir de una muestra. Si se toma una muestra con reemplazamiento de n valores de ella, de entre todos los estimadores posibles de la varianza de la población de partida, existen dos de uso corriente:
de n valores de ella, de entre todos los estimadores posibles de la varianza de la población de partida, existen dos de uso corriente:Propiedades de la varianza muestral
Como consecuencia de la igualdad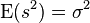 , s2 es un estadístico insesgado de
, s2 es un estadístico insesgado de  . Además, si se cumplen las condiciones necesarias para la ley de los grandes números, s2 es un estimador consistente de
. Además, si se cumplen las condiciones necesarias para la ley de los grandes números, s2 es un estimador consistente de  .
.Más aún, cuando las muestras siguen una distribución normal, por el teorema de Cochran,
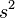 tiene la distribución chi-cuadrado:
tiene la distribución chi-cuadrado: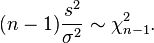
- EJEMPLO
Calcular la varianza de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


EJEMPLO
Calcular la varianza de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60 | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |


3.4 Desviación típica
Desviación típica
La varianza a veces no se interpreta claramente, ya que se mide en unidades cuadráticas. Para evitar ese problema se define otra medida de dispersión, que es la desviación típica, o desviación estándar, que se halla como la raíz cuadrada positiva de la varianza. La desviación típica informa sobre la dispersión de los datos respecto al valor de la media; cuanto mayor sea su valor, más dispersos estarán los datos. Esta medida viene representada en la mayoría de los casos por S, dado que es su inicial de su nominación en inglés.Desviación típica muestral
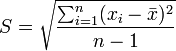
Desviación típica poblacional
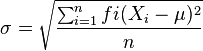
-->x = [17 14 2 5 8 7 6 8 5 4 3 15 9] x = 17. 14. 2. 5. 8. 7. 6. 8. 5. 4. 3. 15. 9. -->stdev(x) ans = 4.716311 -->Primero hemos declarado un vector con nombre X, donde introducimos los números de la serie. Luego con el comando stdev se hallará la desviación típica.
Propiedades de la desviación típica
1 La desviación típica será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.
2 Si a todos los valores de la variable se les suma un número la desviación típica no varía.
3 Si todos los valores de la variable se multiplican por un número la desviación típica queda multiplicada por dicho número.
4 Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones típicas se puede calcular la desviación típica total.
Si todas las muestras tienen el mismo tamaño:

Si las muestras tienen distinto tamaño:

EJEMPLO
Calcular la desviación típica de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


EJEMPLO
Calcular la desviación típica de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60) | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |


3.3 Desviación media
Desviación respecto a la media
La desviación respecto a la media es la diferencia en valor absoluto entre cada valor de la variable estadística y la media aritmética.
Di = |x - x|
Desviación media
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
La desviación media se representa por 



Ejemplo:


Calcular la desviación media de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


Desviación media para datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la desviación media es:


Calcular la desviación media de la distribución:
| xi | fi | xi · fi | |x - x| | |x - x| · fi | |
| [10, 15) | 12.5 | 3 | 37.5 | 9.286 | 27.858 |
|---|---|---|---|---|---|
| [15, 20) | 17.5 | 5 | 87.5 | 4.286 | 21.43 |
| [20, 25) | 22.5 | 7 | 157.5 | 0.714 | 4.998 |
| [25, 30) | 27.5 | 4 | 110 | 5.714 | 22.856 |
| [30, 35) | 32.5 | 2 | 65 | 10.714 | 21.428 |
| 21 | 457.5 | 98.57 |


El primer paso consiste en hallar la media:
Ejemplo
En un partido de baloncesto, se tiene la siguiente anotación en los jugadores de un equipo:Aplicando la fórmula
| Puntuación |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Suscribirse a:
Entradas (Atom)
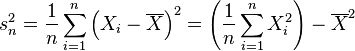
![\operatorname{Var}(X) = \operatorname{E}[ ( X - \mu ) ^ 2].\,](https://upload.wikimedia.org/math/e/1/9/e195b2e01ec2b268ec60233266ad2ecf.png)
![\begin{align}
\operatorname{Var}(X) & = \operatorname{E}[ ( X - \mu ) ^ 2 ] \\
& = \operatorname{E}[ ( X ^ 2 - 2X\mu + \mu ^ 2) ] \\
& = \operatorname{E}[ X ^ 2] - 2\mu\operatorname{E}[X] + \mu ^ 2 \\
& =\operatorname{E}[ X ^ 2] - 2\mu ^ 2 + \mu ^ 2 \\
& = \operatorname{E} [ X ^ 2] - \mu ^ 2.
\end{align}](https://upload.wikimedia.org/math/5/0/a/50a64058b79694b25a95e3dca34441cf.png)
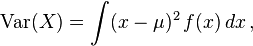
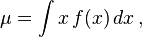
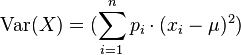

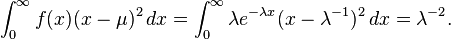
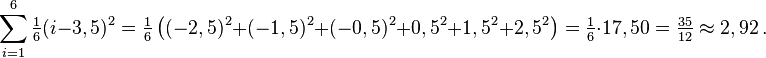
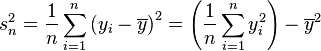
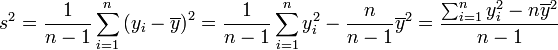
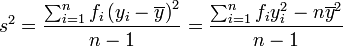
![\begin{align}
\operatorname{E}[s^2] & = \operatorname{E}\left[\frac{1}{n-1} \sum_{i=1}^n Y_i^2 ~ - ~ \frac{n}{n-1} \overline{Y}^2 \right] \\
& = \frac{1}{n-1}\left( \sum \operatorname{E}[Y_i^2] ~ - ~ n \operatorname{E}[\overline{Y}^2] \right) \\
& = \frac{1}{n-1}\left( n \operatorname{E}[Y_1^2] ~ - ~ n \operatorname{E}[\overline{Y}^2] \right) \\
& = \frac{n}{n-1}\left( \operatorname{Var}(Y_1) + \operatorname{E}[Y_1]^2 ~ - ~ \operatorname{Var}(\overline{Y}) - \operatorname{E}[\overline{Y}]^2 \right) \\
& = \frac{n}{n-1}\left( \operatorname{Var}(Y_1) + \mu^2 ~ - ~ \frac{1}{n}\operatorname{Var}(Y_1) - \mu^2 \right) \\
& = \frac{n}{n-1}\left( \frac{n-1}{n} ~ \operatorname{Var}(Y_1) \right) \\
& = \operatorname{Var}(Y_1) \\
& = \sigma^2
\end{align}](https://upload.wikimedia.org/math/f/1/5/f159af80af3cf1b0654e68d1f347ef1c.png)
![E[s_n^2] = \frac{n-1}{n} \sigma^2](https://upload.wikimedia.org/math/8/d/7/8d70d0f4b102b1b1c50ee60bd7bcad11.png)