Frecuencia es una magnitud que mide el
número de repeticiones por unidad de tiempo de cualquier fenómeno o suceso periódico.
Para
calcular la frecuencia de un suceso, se contabilizan un número de ocurrencias
de este teniendo en cuenta un intervalo temporal, luego estas repeticiones se
dividen por el tiempo transcurrido. Según el Sistema Internacional
(SI), la frecuencia se mide en hercios (Hz), en honor a Heinrich Rudolf Hertz.
Un hercio es la frecuencia de un suceso o fenómeno repetido una vez por segundo.
Así, un fenómeno con una frecuencia de dos hercios se repite dos veces por
segundo. Esta unidad se llamó originalmente «ciclo por segundo» (cps).
Otras unidades para indicar frecuencias son revoluciones por minuto (rpm o r/min según la notación del SI. Las pulsaciones del corazón se miden en latidos por minuto (lat/min) y el tempo musical se mide en «pulsos por minuto» (bpm, del inglés “beats per minute”).
Otras unidades para indicar frecuencias son revoluciones por minuto (rpm o r/min según la notación del SI. Las pulsaciones del corazón se miden en latidos por minuto (lat/min) y el tempo musical se mide en «pulsos por minuto» (bpm, del inglés “beats per minute”).

Un método
alternativo para calcular la frecuencia es medir el tiempo entre dos
repeticiones (periodo) y
luego calcular la frecuencia (f) recíproca de esta manera:
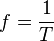
donde T
es el periodo de la señal.
Frecuencias de ondas
Dos
frecuencias y , una de «ritmo» superior a la otra.
La
frecuencia tiene una relación inversa con el concepto de longitud de onda (ver gráfico), a mayor
frecuencia menor longitud de onda y viceversa. La frecuencia f es igual
a la velocidad v de la onda, dividido por la
longitud de onda λ (lambda):
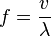
Cuando
las ondas viajan de un medio a otro, como por ejemplo de aire
a agua, la frecuencia de la onda se mantiene
constante, cambiando sólo su longitud , de onda y la velocidad.
Por el efecto Doppler, la frecuencia es una magnitud
invariable en el universo. Es decir, no se
puede modificar por ningún proceso físico excepto por su velocidad de
propagación o longitud de onda.
Frecuencia
absoluta ni Es la frecuencia ya aplicada en la primera tabla, que corresponde
al número de veces que se repite un dato dentro un rango dado, según sea
definido previamente.
Frecuencia
absoluta acumulada (Ni) Es el número de veces ni en la muestra de N, con un
valor igual o menor al de la variable. La última frecuencia absoluta acumulada
deberá ser igual a N.
Frecuencia
relativa (fi) Es el cociente entre la frecuencia absoluta y el tamaño de la
muestra (N), para cada valor de i en la tabla, según la fórmula: fi = ni / N
Frecuencia
relativa acumulada (Fi) Es el cociente entre la frecuencia absoluta acumulada y
el número total de datos, N. Es decir, Fi = Ni / N.
Frecuencia de la corriente alterna
Voltaje y frecuencia: 220-240 V/60 Hz 220-240
V/50 Hz 100-127 V/60 Hz 100-127
V/50 Hz
En Europa, Asia,
Oceanía, África y gran parte de América del Sur, la
frecuencia de corriente alterna
para uso doméstico (en electrodomésticos,
etc.) es de 50 Hz. En cambio en América del Norte
de 60 Hz.
Para
determinar la frecuencia de la corriente alterna producida por un generador
eléctrico se utiliza la siguiente ecuación:
F= P•Vg/120
Donde:
F: frecuencia (en Hz)
P: número de polos (siempre deben
ser pares)
Vg: velocidad de giro
(en rpm).
otra
manera de calcular la frecuencia de la corriente alterna producida por un
generador eléctrico:
F=P•Vg/60
Donde:
F: frecuencia (en Hz)
P: número de pares de polos.
Vg: velocidad de giro
(en rpm).
Longitudes de onda
De acuerdo
a lo indicado anteriormente, la longitud de onda tiene una relación inversa con
la frecuencia, a mayor frecuencia, menor longitud de onda, y viceversa. La
longitud de onda λ (lambda) es igual a la velocidad v de la onda,
dividido por la frecuencia f:
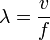
Una onda
electromagnética de 2 milihercios tiene una
longitud de onda aproximadamente igual a la distancia de la Tierra al Sol
(150 millones de kilómetros). Una onda electromagnética de 1 microhercio tiene una longitud de onda de
0,0317 años luz. Una onda
electromagnética de 1 nanohercio tiene una
longitud de onda de 31,69 años luz
Ejemplos :
Durante el mes de julio, en una ciudad se han registrado las siguientes temperaturas máximas:
32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30, 30, 29, 29, 30, 30, 31, 30, 31, 34, 33, 33, 29, 29.
Construir la tabla de frecuencias.
| xi | fi | Fi | ni | Ni |
|---|---|---|---|---|
| 27 | 1 | 1 | 0.032 | 0.032 |
| 28 | 2 | 3 | 0.065 | 0.097 |
| 29 | 6 | 9 | 0.194 | 0.290 |
| 30 | 7 | 16 | 0.226 | 0.516 |
| 31 | 8 | 24 | 0.258 | 0.774 |
| 32 | 3 | 27 | 0.097 | 0.871 |
| 33 | 3 | 30 | 0.097 | 0.968 |
| 34 | 1 | 31 | 0.032 | 1 |
| 31 | 1 |
2.Los pesos de los 65 empleados de una fábrica vienen dados por la siguiente tabla:
| Peso | fi |
| [50, 60) | 8 |
| [60, 70) | 10 |
| [70, 80) | 16 |
| [80,90) | 14 |
| [90, 100) | 10 |
| [100, 110) | 5 |
| [110, 120) | 2 |
Construir la tabla de frecuencias.
| xi | fi | Fi | ni | Ni | |
| [50, 60) | 55 | 8 | 8 | 0.12 | 0.12 |
| [60, 70) | 65 | 10 | 18 | 0.15 | 0.27 |
| [70, 80) | 75 | 16 | 34 | 0.24 | 0.51 |
| [80,90) | 85 | 14 | 48 | 0.22 | 0.73 |
| [90, 100) | 95 | 10 | 58 | 0.15 | 0.88 |
| [100, 110) | 105 | 5 | 63 | 0.08 | 0.96 |
| [110, 120) | 115 | 2 | 65 | 0.03 | 0.99 |
| 65 |
3.Un
dentista observa el número de caries en cada uno de los 100 niños de
cierto colegio. La información obtenida a parecer resumida en la
siguiente tabla:
| Nº de caries | fi | ni |
| 0 | 25 | 0.25 |
| 1 | 20 | 0.2 |
| 2 | x | z |
| 3 | 15 | 0.15 |
| 4 | y | 0.05 |
Completar la tabla obteniendo los valores x, y, z.
La suma de las frecuencias relativas ha de ser igual a 1:
0.25 + 0.2 + z + 0.15 + 0.05 = 1
0.65 + z = 1 z = 0.35
La frecuencia relativa de un
dato es igual su frecuencia absoluta dividida entre 100, que es la suma
de las frecuencias absolutas.
| Nº de caries | fi | ni | fi · ni |
| 0 | 25 | 0.25 | 0 |
| 1 | 20 | 0.2 | 20 |
| 2 | 35 | 0.35 | 70 |
| 3 | 15 | 0.15 | 45 |
| 4 | 5 | 0.05 | 20 |
| 155 |


la tabla del Ni
ResponderEliminar