3.4 Desviación típica

Desviación típica

La varianza a veces no se interpreta claramente, ya que se mide en unidades cuadráticas. Para evitar ese problema se define otra medida de dispersión, que es la desviación típica, o desviación estándar, que se halla como la raíz cuadrada positiva de la varianza. La desviación típica informa sobre la dispersión de los datos respecto al valor de la media; cuanto mayor sea su valor, más dispersos estarán los datos. Esta medida viene representada en la mayoría de los casos por S, dado que es su inicial de su nominación en inglés.

Desviación típica muestral

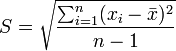
Desviación típica poblacional

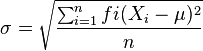
-->x = [17 14 2 5 8 7 6 8 5 4 3 15 9]
x = 17. 14. 2. 5. 8. 7. 6. 8. 5. 4. 3. 15. 9.
-->stdev(x)
ans = 4.716311
-->

Primero hemos declarado un vector con nombre X, donde introducimos los números de la serie. Luego con el comando stdev se hallará la desviación típica.

Propiedades de la desviación típica

1 La desviación típica será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.

2 Si a todos los valores de la variable se les suma un número la desviación típica no varía.

3 Si todos los valores de la variable se multiplican por un número la desviación típica queda multiplicada por dicho número.

4 Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones típicas se puede calcular la desviación típica total.

Si todas las muestras tienen el mismo tamaño:

Si las muestras tienen distinto tamaño:

  EJEMPLO

Calcular la desviación típica de la distribución:

9, 3, 8, 8, 9, 8, 9, 18

 

                                                                      EJEMPLO

Calcular la desviación típica de la distribución de la tabla:

	xi	fi	xi · fi	xi2 · fi
[10, 20)	15	1	15	225
[20, 30)	25	8	200	5000
[30,40)	35	10	350	12 250
[40, 50)	45	9	405	18 225
[50, 60)	55	8	440	24 200
[60,70)	65	4	260	16 900
[70, 80)	75	2	150	11 250
		42	1 820	88 050