viernes, 26 de junio de 2015

2.4 Media geométrica

En matemáticas y estadística, la media geométrica de una cantidad arbitraria de números (por decir n números) es la raíz n-ésima del producto de todos los números, es recomendada para datos de progresión geométrica, para promediar razones, interés compuesto y números índices.
\bar{x} = \sqrt[n]{\prod_{i=1}^n{x_i}} = \sqrt[n]{x_1 \cdot x_2 \cdots x_n}
Por ejemplo, la media geométrica de 2 y 18 es
\sqrt[2]{2 \cdot 18} = \sqrt[2]{36} = 6
Otro ejemplo, la media de 1, 3 y 9 sería
\sqrt[3]{1 \cdot 3 \cdot 9} = \sqrt[3]{27} = 3  
 
                              Dibujo de la media geométrica

Propiedades

  • El logaritmo de la media geométrica es igual a la media aritmética de los logaritmos de los valores de la variable.
  • La media geométrica de un conjunto de números positivos es siempre menor o igual que la media artimética:
(x_1 x_2 \dots x_n)^{\frac{1}{n}} \le \frac{x_1+ x_2 +\dots + x_n}{n}
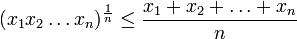
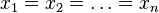La igualdad sólo se alcanza si x_1 = x_2 = \dots = x_n.
Ventajas
  • considera todos los valores de la distribución y
  • es menos sensible que la media aritmética a los valores extremos.
Desventajas
  • es de significado estadístico menos intuitivo que la media aritmética,
  • su cálculo es más difícil y
  • en ocasiones no queda determinada; por ejemplo, si un valor x_i = 0 \, entonces la media geométrica se anula.
Solo es relevante la media geométrica si todos los números son positivos. Como hemos visto, si uno de ellos es 0, entonces el resultado es 0. Si hubiera un número negativo (o una cantidad impar de ellos) entonces la media geométrica sería o bien negativa, o bien inexistente en los números reales.
En muchas ocasiones se utiliza su trasformación en el manejo estadístico de variables con distribución no normal.
La media geométrica es relevante cuando varias cantidades son multiplicadas para producir un total.

Media geométrica ponderada

Al igual que en una media aritmética pueden introducirse pesos como valores multiplicativos para cada uno de los valores con el fin de ponderar o hacer pesar más en el resultado final ciertos valores, en la media geométrica pueden introducirse pesos como exponentes:
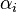\bar{x} = \left({\prod_{i=1}^n{x_i}^{\alpha_i}}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}}
Donde las \alpha_i \, son los «pesos».

Caso ilustrativo

Una cadena de expendedores de gasolina el año pasado aumentó sus ingresos respecto al año anterior en 21%; y han proyectado que este año van a llegar a un aumento de 28% con respecto al año pasado. ¿Cuánto es el promedio anual del aumento porcentual?
Definitivamente no es (21% + 28%):2 = 24,5%.
El monto de la producción, al final de dos años, es 100(1,21)(1,28)= 154,88. Si en cada año se tuviera una tasa anual de aumento de i% resulta
100 → 100(1+i) → 100(1 +i)2.
Entonces
100(1 +i)2 = 154,88
(1 +i)2 = 1,5488
1 + i = 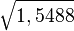\sqrt{1,5488} =1,244507
i = 0,244507 = 24,451% 

Dónde ocurre

Geometría

  • la altura de un triángulo rectángulo cumple 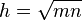h =\sqrt{mn}, siendo m y n las proyecciones de los catetos sobre la hipotenusa.
  • un cateto b cumple b =\sqrt{ma} m su proyección y a la hipotenusa.
  • la tangente t a una circunferencia 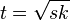t =\sqrt{sk} , s es secante y k la parte interna.
  • el lado de un cuadrado equivalente a un rectángulo es la media geométrica de los lados de este; el radio de un círculo equivalente a una elipse es la media geométrica de los semiejes de esta. Lo mismo el caso de la esfera con la elipsoide
  • el lado (arista) d de un cubo equivalente a un ortoedro de lados a, b, c es d =\sqrt[3]{abc} 2

Pesas

El peso w de una sustancia que tiene pesos hallados por dos balanzas u y v , resulta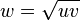 w =\sqrt{uv} 3

 EJEMPLO
Supongase que las utilidades obtenidas por una compañía constructora en cuatro proyectos fueron de 3, 2, 4 y 6%, respectivamente. ¿ Cúal es la media geométrica de las ganancias?.
En este ejemplo y asi la media geométrica es determinada por
y así la media geométrica de las utilidades es el 3.46%.
La media aritmética de los valores anteriores es 3.75%. Aunque el valor 6% no es muy grande, hace que la media aritmética se incline hacia valores elevados. La media geométrica no se ve tan afectada por valores extremos. 

                  Dibujo en barras del cálculo de la media geométrica del porcentaje de mujeres en los cinco principales departamentos de una empresa 

EJEMPLO

Supongase que las utilidades obtenidas por una compañía constructora en cuatro proyectos fueron de 3, 2, 4 y 6%, respectivamente. ¿ Cúal es la media geométrica de las ganancias?.
En este ejemplo y asi la media geométrica es determinada por
y así la media geométrica de las utilidades es el 3.46%.
La media aritmética de los valores anteriores es 3.75%. Aunque el valor 6% no es muy grande, hace que la media aritmética se incline hacia valores elevados. La media geométrica no se ve tan afectada por valores extremos.

 
Publicado por en

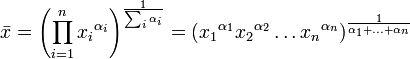
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)