2.3 MODA

En estadística, la moda es el valor con una mayor frecuencia en una distribución de datos.
Se hablará de una distribución bimodal de los datos adquiridos en una columna cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es en la que encontramos tres modas. Si todas las variables tienen la misma frecuencia diremos que no hay moda.
El intervalo modal es el de mayor frecuencia absoluta. Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal.
La moda, cuando los datos están agrupados, es un punto que divide al intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:

Siendo la frecuencia absoluta del intervalo modal las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al intervalo modal.

Moda de datos agrupados

Para obtener la moda en datos agrupados se usa la siguiente fórmula:

Donde:

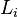= _{-inferior de la clase modal}.

= es el delta de frecuencia absoluta modal y la frecuencia absoluta premodal.

= es el delta de frecuencia absoluta modal y la frecuencia absoluta postmodal.

= Amplitud del intervalo modal

Propiedades

Sus principales propiedades son:

• Cálculo sencillo.
• Interpretación muy clara.
• Al depender sólo de las frecuencias, puede calcularse para variables cualitativas. Es por ello el parámetro más utilizado cuando al resumir una población no es posible realizar otros cálculos, por ejemplo, cuando se enumeran en medios periodísticos las características más frecuentes de determinado sector social. Esto se conoce informalmente como "retrato robot".

Inconvenientes

• Su valor es independiente de la mayor parte de los datos, lo que la hace muy sensible a variaciones muestrales. Por otra parte, en variables agrupadas en intervalos, su valor depende excesivamente del número de intervalos y de su amplitud.
• Usa muy pocas observaciones, de tal modo que grandes variaciones en los datos fuera de la moda, no afectan en modo alguno a su valor.
• No siempre se sitúa hacia el centro de la distribución.
• Puede haber más de una moda en el caso en que dos o más valores de la variable presenten la misma frecuencia (distribuciones bimodales o multimodales)

 

 

                                                     EJEMPLOS 

Calcular la moda de una distribución estadística que viene dada por la siguiente tabla:

	fi
[60, 63)	5
[63, 66)	18
[66, 69)	42
[69, 72)	27
[72, 75)	8
	100

 

En la siguiente tabla se muestra las calificaciones (suspenso, aprobado, notable y sobresaliente) obtenidas por un grupo de 50 alumnos. Calcular la moda.

	fi	hi
[0, 5)	15	3
[5, 7)	20	10
[7, 9)	12	6
[9, 10)	3	3
	50