En teoría de probabilidad, la varianza (que suele representarse como
 ) de una variable aleatoria es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media.
) de una variable aleatoria es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media.Está medida en unidades distintas de las de la variable. Por ejemplo, si la variable mide una distancia en metros, la varianza se expresa en metros al cuadrado. La desviación estándar es la raíz cuadrada de la varianza, es una medida de dispersión alternativa expresada en las mismas unidades de los datos de la variable objeto de estudio. La varianza tiene como valor mínimo 0.
Hay que tener en cuenta que la varianza puede verse muy influida por los valores atípicos y no se aconseja su uso cuando las distribuciones de las variables aleatorias tienen colas pesadas. En tales casos se recomienda el uso de otras medidas de dispersión más robustas.
Definición
Si tenemos un conjunto de datos de una misma variable, la varianza se calcula de la siguiente forma: : cada dato
: cada dato : El número de datos
: El número de datos : la media aritmética de los datos
: la media aritmética de los datos
Variable aleatoria
Aplicando este concepto a una variable aleatoria con media μ = E[X], se define su varianza, Var(X) (también representada como o, simplemente σ2), como
o, simplemente σ2), comoCaso continuo
Si la variable aleatoria X es continua con función de densidad f(x), entoncesCaso discreto
Si la variable aleatoria X es discreta con pesos x1 ↦ p1, ..., xn ↦ pn y n es la cantidad total de datos, entonces tenemos: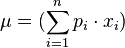 .
.
Ejemplos
Distribución exponencial
La distribución exponencial de parámetro λ es una distribución continua con soporte en el intervalo [0,∞) y función de densidadDado perfecto
Un dado de seis caras puede representarse como una variable aleatoria discreta que toma, valores del 1 al 6 con probabilidad igual a 1/6. El valor esperado es (1+2+3+4+5+6)/6 = 3,5. Por lo tanto, su varianza es:Propiedades de la varianza
Algunas propiedades de la varianza son: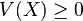
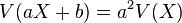 siendo a y b números reales cualesquiera. De esta propiedad se deduce que la varianza de una constante es cero, es decir,
siendo a y b números reales cualesquiera. De esta propiedad se deduce que la varianza de una constante es cero, es decir, 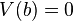
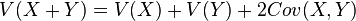 , donde Cov(X,Y) es la covarianza de X e Y.
, donde Cov(X,Y) es la covarianza de X e Y.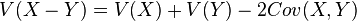 , donde Cov(X,Y) es la covarianza de X e Y.
, donde Cov(X,Y) es la covarianza de X e Y.
Varianza muestral
En muchas situaciones es preciso estimar la varianza de una población a partir de una muestra. Si se toma una muestra con reemplazamiento de n valores de ella, de entre todos los estimadores posibles de la varianza de la población de partida, existen dos de uso corriente:
de n valores de ella, de entre todos los estimadores posibles de la varianza de la población de partida, existen dos de uso corriente:Propiedades de la varianza muestral
Como consecuencia de la igualdad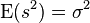 , s2 es un estadístico insesgado de
, s2 es un estadístico insesgado de  . Además, si se cumplen las condiciones necesarias para la ley de los grandes números, s2 es un estimador consistente de
. Además, si se cumplen las condiciones necesarias para la ley de los grandes números, s2 es un estimador consistente de  .
.Más aún, cuando las muestras siguen una distribución normal, por el teorema de Cochran,
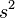 tiene la distribución chi-cuadrado:
tiene la distribución chi-cuadrado: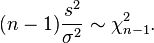
- EJEMPLO
Calcular la varianza de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
EJEMPLO
Calcular la varianza de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60 | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
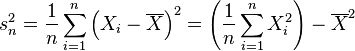
![\operatorname{Var}(X) = \operatorname{E}[ ( X - \mu ) ^ 2].\,](https://upload.wikimedia.org/math/e/1/9/e195b2e01ec2b268ec60233266ad2ecf.png)
![\begin{align}
\operatorname{Var}(X) & = \operatorname{E}[ ( X - \mu ) ^ 2 ] \\
& = \operatorname{E}[ ( X ^ 2 - 2X\mu + \mu ^ 2) ] \\
& = \operatorname{E}[ X ^ 2] - 2\mu\operatorname{E}[X] + \mu ^ 2 \\
& =\operatorname{E}[ X ^ 2] - 2\mu ^ 2 + \mu ^ 2 \\
& = \operatorname{E} [ X ^ 2] - \mu ^ 2.
\end{align}](https://upload.wikimedia.org/math/5/0/a/50a64058b79694b25a95e3dca34441cf.png)
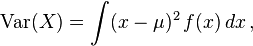
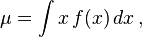
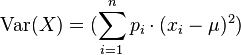

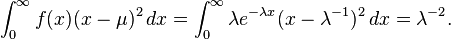
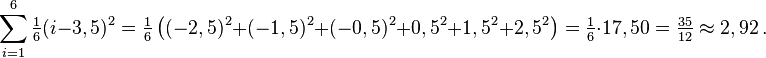
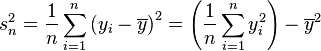
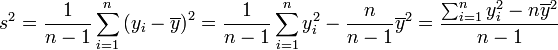
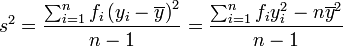
![\begin{align}
\operatorname{E}[s^2] & = \operatorname{E}\left[\frac{1}{n-1} \sum_{i=1}^n Y_i^2 ~ - ~ \frac{n}{n-1} \overline{Y}^2 \right] \\
& = \frac{1}{n-1}\left( \sum \operatorname{E}[Y_i^2] ~ - ~ n \operatorname{E}[\overline{Y}^2] \right) \\
& = \frac{1}{n-1}\left( n \operatorname{E}[Y_1^2] ~ - ~ n \operatorname{E}[\overline{Y}^2] \right) \\
& = \frac{n}{n-1}\left( \operatorname{Var}(Y_1) + \operatorname{E}[Y_1]^2 ~ - ~ \operatorname{Var}(\overline{Y}) - \operatorname{E}[\overline{Y}]^2 \right) \\
& = \frac{n}{n-1}\left( \operatorname{Var}(Y_1) + \mu^2 ~ - ~ \frac{1}{n}\operatorname{Var}(Y_1) - \mu^2 \right) \\
& = \frac{n}{n-1}\left( \frac{n-1}{n} ~ \operatorname{Var}(Y_1) \right) \\
& = \operatorname{Var}(Y_1) \\
& = \sigma^2
\end{align}](https://upload.wikimedia.org/math/f/1/5/f159af80af3cf1b0654e68d1f347ef1c.png)
![E[s_n^2] = \frac{n-1}{n} \sigma^2](https://upload.wikimedia.org/math/8/d/7/8d70d0f4b102b1b1c50ee60bd7bcad11.png)
No hay comentarios:
Publicar un comentario